Quantum Cryptographic Threat Timeline
Threat Timeline
The rise of the Distributed Denial of Secrets group and the fall of Wikileaks have not escaped those IT departments all over the world, which are tasked with caring for the security of their organization’s databases. To the hacktivists, who want to expose an organization’s actions, the organization’s databases are fair game.
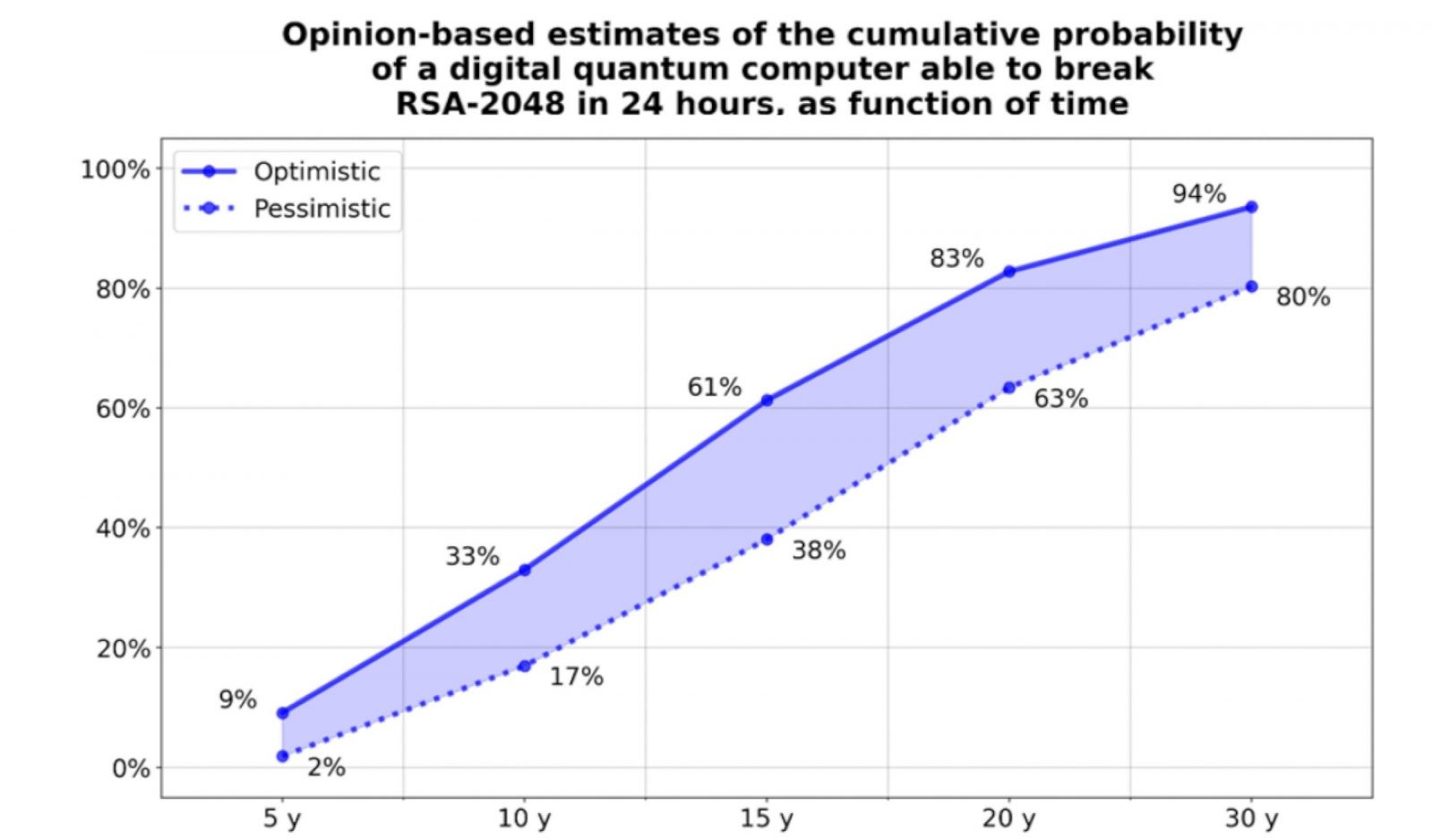
Despite your safe computing, and non-nefarious activities, your organization’s computers’ databases can still be hacked, with your data saved for the hackers’ long game, to later break its security. How long? An estimate from experts in the “post- quantum cryptography” – PQC – field; suggest an average of fifteen years, with ranges, seen in Fig. 1.
That fifteen years’ middle estimate emerged from the most recent annual assessment, the “2021 Quantum Threat Timeline Report”, written by Michele Mosca (Co-Founder & CEO, evolutionQ Inc.) and Marco Piani, (Senior Research Analyst, evolutionQ Inc.) and published by the Global Risk Institute. If you are an organization manager, you need this report in your forecasting toolkit, as it reflects the views of nearly fifty quantum computing experts about the field’s scientific or technological developments and tracks their opinions over time.
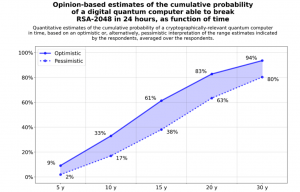
Figure 1. An aggregated likelihood of the experts’ answers using optimistic and pessimistic ranges, averaged over the respondents’ answers. Reproduced from Figure 15 of the 2021 full Quantum Threat Timeline Report.
Mosca’s Theorem to Rule Them All
With a nod to the author: J.R.R. Tolkien, we cannot escape the report’s co-author’s implicit concept: “Mosca’s Theorem”: “If x + y > z , then worry”, which states that if quantum computers become powerful enough before time: x+y, then your data may be exposed while it is still sensitive. The variables: x years = the time that you need encryption to be secure, y years = the time to re-tool the existing infrastructure with large-scale quantum-safe solution, and z = the time for a large-scale quantum computer to be built.
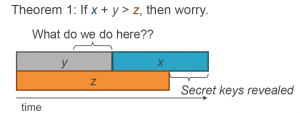
Figure 2. Illustration of Mosca’s Theorem from page 21 of Mosca’s 2015 presentation: Cyber security in a Quantum World: Will We be Ready?
If you need to convince others to begin your organization’s transition, a less mathematical version of Mosca’s theorem is represented in Fig. 3.
Figure 3. Illustration of Mosca’s Theorem reproduced from Figure 1 of the Global Risk Institute’s 2021 full Quantum Threat Timeline Report by Mosca and Piani.
NIST to the Rescue
Mosca’s theorem in 2015 formed part of the 2016 justification for the National Institute of Standards and Technology’s (NIST) own PQC strategy to establish a handful of PQC algorithms with the international community (Google groups: pqc-forum). The Round 3 candidates were announced July 22, 2020, with the final selection expected to occur later in 2021. As that event hasn’t happened yet (April 2022), here are two status reports, the first is detailed, and the second, is a brief note.
NIST @ PKC 2022
Dustin Moody, of NIST’s PQC group, gave a one-hour, invited talk at the March 2022, PKC 2022 conference, titled: The Beginning of the End: The First NIST PQC Standards [available at YouTube / pdf, 31 Slides]. It was an information-rich talk that 1) described the NIST PQC standardization process, 2) what’s happened during the last six years and, 3) NIST’s call for quantum-resistant cryptographic algorithms for new public-key crypto standards.
Why do we need new cryptographic standards? Short answer: Shor’s and Grover’s algorithms.
The current NIST standards that form the basis of public key cryptography (PKC) are based on the assumption that there is no polynomial time classical algorithm that solves the integer factorization and discrete logarithm problems of PKC.
However, Shor in 1994, [Shor94] found an efficient quantum algorithm for solving these two problems, which would destroy the security basis for most real deployed PKC systems when (not if!) large-scale quantum computers become available. Moreover, Grover in 1996, described a polynomial speed-up in structured searches from O(N) to O(sqrt(N)), with this astonishingly prescient PQC-relevant sentence:
“It might be possible to combine the search scheme of this paper with [Shor94] and other quantum mechanical algorithms to design faster algorithms”.
Therefore, Moody said that these: Asymmetric Key Algorithms must be replaced by quantum cryptographic algorithms, due to Shor’s algorithm:
- SP800-56A: Diffie-Hellman, ECDH
- SP 800-56B: RSA encryption
- FIPS 186: RSA, DSA, and ECDSA signatures
And that these Symmetric Key algorithms: (AES, SHA), would be affected by Grover’s algorithm, but less dramatically.
NIST will not pick a single “winner”; ideally, several algorithms will emerge as good choices, and that they must worry about classical and quantum computers. Moody described NIST’s Selection Criteria, Security Categories, and what are the 3rd Round finalists and Alternates. The Finalists are those most promising algorithms to be ready for standardization at the end of 3rd round, and the Alternates, are those candidates for potential standardization, most likely after another (4th) round. Result: 7 Finalists and 8 Alternates.
With “key encapsulation mechanisms (KEM)”, defined as those used to secure symmetric key material for transmission by using asymmetric (public-key) algorithms, NIST’s 3rd Round Finalists and Alternates are:
- KEM finalists: Kyber, NTRU, SABER, Classic McEliece
- Signature finalists: Dilithium, Falcon, Rainbow
- KEM alternates: BIKE, FrodoKEM, HQC, NTRUprime, SIKE
- Signature alternates: GeMSS, Picnic, SPHINCS+
Moody said that the 3rd Round will end any day now. NIST will announce which finalist algorithms it will standardize, with a Report on the 3rd Round to explain their decisions. NIST will also announce any candidates advancing to 4th round (next 18-24 months)
Of the algorithm types, post-quantum cryptographers will recognize the same categories in this well-cited (710 citations, 2009) Post-Quantum Cryptography book, by editors: Bernstein, Buchmann, and Dahmen. I also recommend: Cryptography 101 From Theory to Practice by Rolf Oppliger (2021), in which many of these algorithms are identified.
- Lattice-based: Specified on a point lattice, must solve problem of type: such as the shortest vector problem (SVP), the closest vector problem (CVP);
- Code-based: based on error-correcting code, private and public keys algorithms different;
- Multivariate-based: Based on finding a solution for multivariate quadratic equations over a finite field;
- Stateless hash: One-time signature system that uses only cryptographic hash functions;
- Isogeny: Uses a nonconstant map between elliptic curves that can be written as a fraction of polynomials
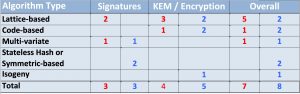
Table 1. NIST’s breakdown of the 3rd Round finalists and Alternates from Slide 16 of Dustin Moody’s PKC 2022 talk.
NIST @ pqc-forum
As the ‘any day now’ has taken some time, Dustin Moody said, on April 19: “We appreciate your patience. The announcement of the algorithms we will standardize is still coming very soon. This is a major milestone of our project, and the delay is not due to technical considerations but is due to some legal and procedural steps that are taking more time than we anticipated.“
Dustin Moody’s presentation states (slide 25) that there are Patent and IPR issues. If I were to guess, this is the reason for the delay.
Amara Graps, Ph.D. is an interdisciplinary physicist, planetary scientist, science communicator and educator and expert on all quantum technologies.





















