(IEEE.Explore) In a groundbreaking study, researchers have derived analytical solutions to the guesswork problem for quantum ensembles
A quantum ensemble—a set of quantum states with their corresponding probabilities—is essential to the encoding of classical information for transmission over quantum channels. But receivers must be able to ‘guess’ the transmitted quantum state, incurring a cost called ‘guesswork.’ Recently, researchers have derived analytical solutions of the guesswork problem for when the ensemble is subject to a finite set of conditions. The results constitute a first step towards future algorithms for quantum software.
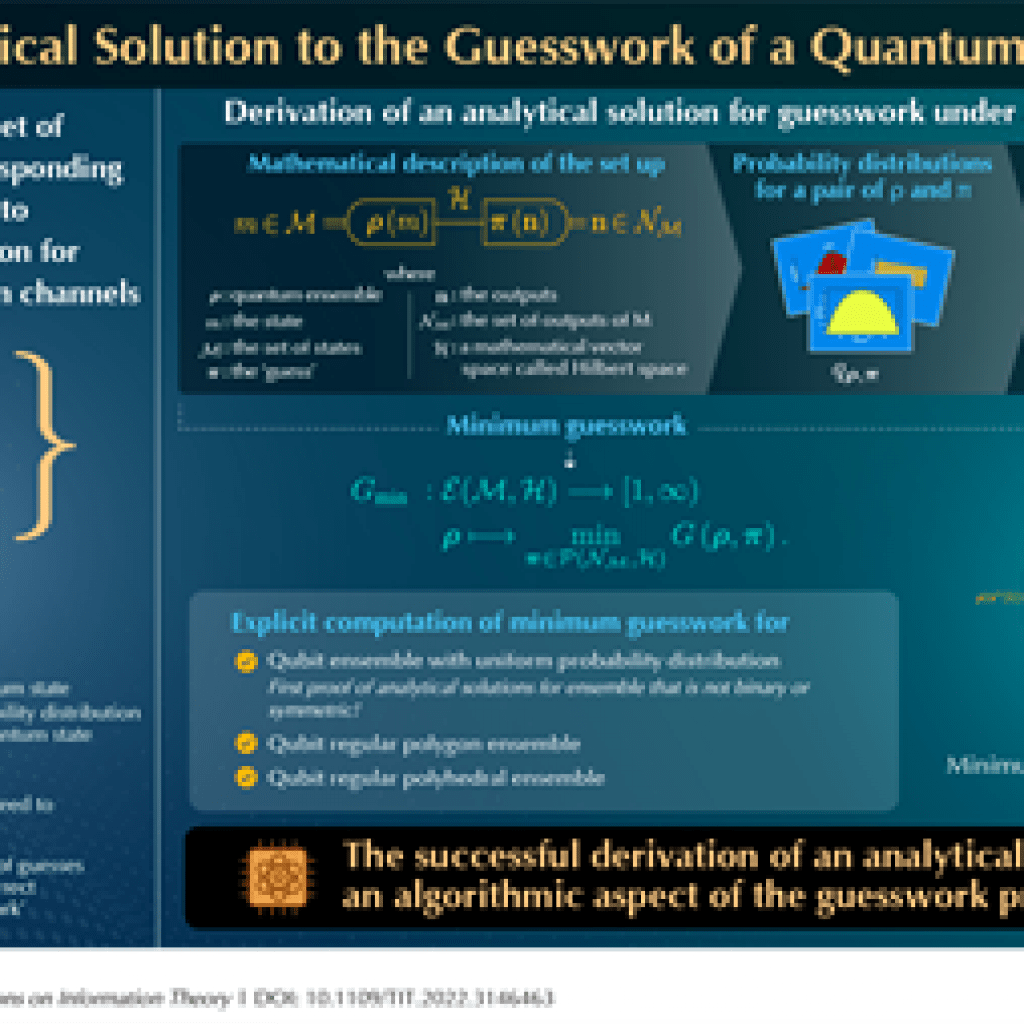
. A quantum ensemble refers to a set of quantum states, each with its own probability. To accurately receive the transmitted information, the receiver has to repeatedly ‘guess’ the state of the information being sent. This constitutes a cost function that is called ‘guesswork.’ Guesswork refers to the average number of guesses required to correctly guess the state.
The concept of guesswork has been studied at length in classical ensembles, but the subject is still new for quantum ensembles. Recently, a research team from Japan—consisting of Prof. Takeshi Koshiba of Waseda University, Michele Dall’Arno from Waseda University and Kyoto University, and Prof. Francesco Buscemi from Nagoya University—has derived analytical solutions to the guesswork problem subject to a finite set of conditions. “The guesswork problem is fundamental in many scientific areas in which machine learning techniques or artificial intelligence are used. Our results trailblaze an algorithmic aspect of the guesswork problem,” says Koshiba.
To begin with, the researchers considered a common formalism of quantum circuits that relates the transmitted state of a quantum ensemble ρ to the quantum measurement π. They next introduced the probability distributions for both the quantum ensemble and the numberings obtained from the quantum measurement. They then established the guesswork function. The guesswork function maps any pair of ρ and π into the expectation value of the tth guess (where t refers to the guess number), averaged over the probability distribution of the tth guess being correct. Finally, they minimized the guesswork function over the elements of π and used this result to derive analytical solutions to the guesswork problem subject to a finite set of conditions.
These solutions included the explicit solution to a qubit ensemble with a uniform probability distribution. “Previously, results for analytical solutions have been known only for binary and symmetric ensembles. Our calculation for ensembles with a uniform probability distribution extends these,” explains Koshiba. The research team also calculated the solutions for a qubit regular polygonal ensemble, and a qubit regular polyhedral ensemble.
“Guesswork is a very basic scientific problem, but there is very little research on quantum guesswork and even less on the algorithmic implications of quantum guesswork. Our paper goes a little way towards filling that gap,” concludes Koshiba.
While the consequences of these findings may not be immediately obvious, in the future they are sure to have a major influence on quantum science, such as quantum chemistry for drug development and quantum software for quantum computing.
Minimizing the guesswork of a quantum ensemble