The 6-qubit IQM Deneb has an operation I guarantee you’ve never seen before on a quantum computer. It’s called MOVE, and I like it.
Inspiration
The inspiration for IQM Deneb came from wanting to “efficiently simulate the dynamics of nanoscale NMR systems.” The team proposed the quantum equivalent of an application-specific integrated chip (ASIC) to do it, which they call a “Co-Design quantum computer.” In other words, IQM Deneb is specially designed to solve problems related to NMR. These problems have real-world applications in biology, chemistry, material science, and medicine. And if you read the paper, there is also an interesting relationship with solid-state quantum sensing, using nitrogen-vacancy centers (NVC) in diamond to achieve nanoscale resolution of the detection and control of nuclear spins.
Despite the special purpose for which IQM Deneb was originally intended, it is still a universal superconducting quantum computer. But if you can imagine a superconducting quantum computer with all-to-all connectivity, like using a quantum computer simulator, that’s IQM Deneb. Sort of.
Native vs. Non-Native
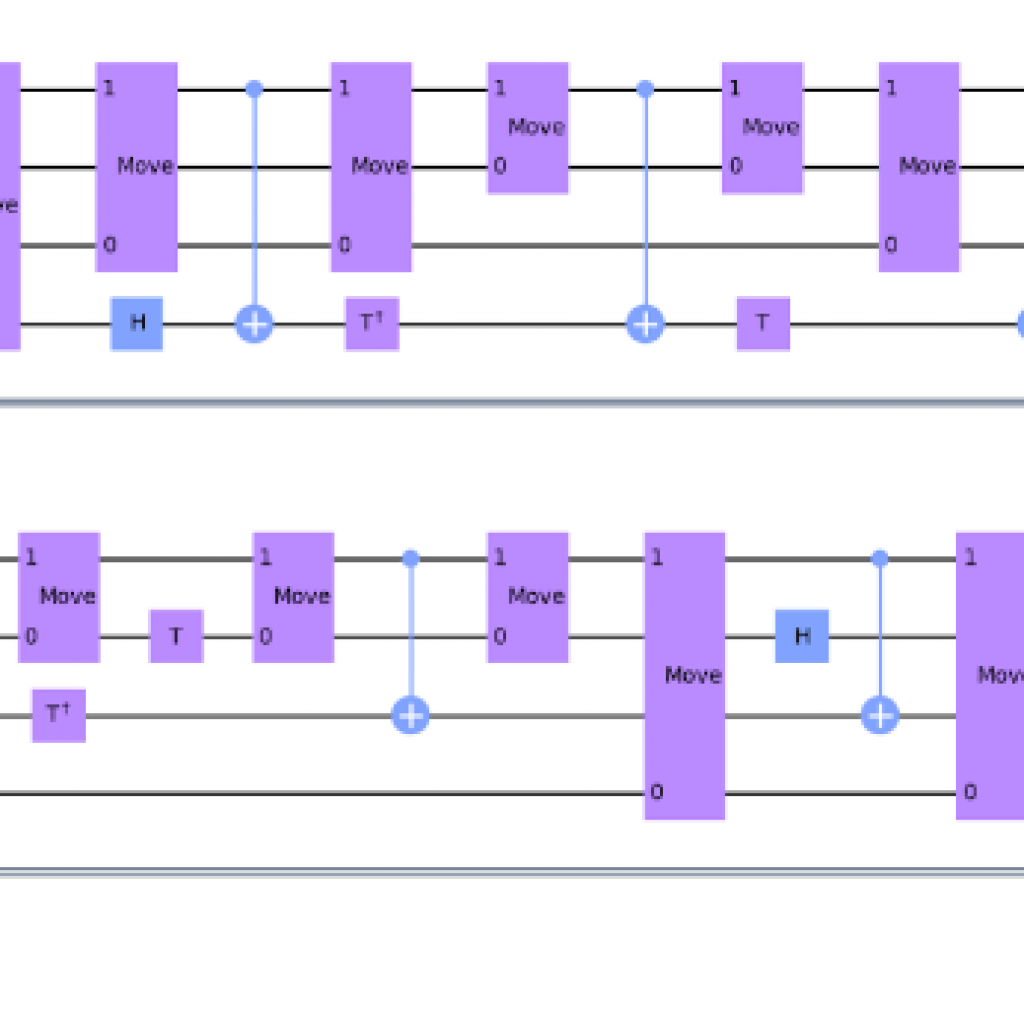
IQM Deneb doesn’t have true all-to-all connectivity, but it has its qubits arranged around a central resonator. You MOVE a qubit to the central resonator, from where CZ gates can be applied to any or all of the other qubits. You then MOVE the qubit back to perform single-qubit operations, as well as to MOVE other qubits, one at a time, to the central resonator.
Although the logical action is different, the MOVE has identical physics to an iSWAP operation. MOVEs and iSWAPs differ from SWAPs in that they are native, whereas SWAP gates are not native and require three noisy CNOT operations to implement. The central resonator only permits MOVE and CZ operations, while the qubits only permit MOVE and single-qubit operations. All qubit connectivity, therefore, depends on the central resonator.
IQM characterizes two MOVEs as being equivalent to one SWAP, but that characterization shortchanges the MOVE. Depending on the connectivity of a superconducting quantum computer, one SWAP on your quantum circuit might actually require several SWAPs on real hardware. But when you MOVE a qubit to the central resonator, it has all-to-all connectivity and does not require anything additional. One MOVE pair is sufficient.
Scalability
The size of the central resonator forces the qubits to be spaced apart more than usual, which has the benefit of reducing crosstalk among them. IQM estimates that they ought to be able to scale the processor in a 1:20 ratio of central resonators to qubits. And much like a superconducting qubit would normally be connected to more than one other qubit, a qubit can also potentially be connected to more than one central resonator, allowing connectivity with more than 20 qubits.
Transpilation
With the disclaimer that the transpiler is not yet optimized, it nonetheless finds interesting efficiencies already. Like other transpilers, it slides single-qubit operations as far left as it can. But what’s interesting is the number of CZ gates it can find to apply when a qubit is in the central resonator. Even if the count of CZ gates can’t be reduced, it seeks to minimize the number of times the qubits have to MOVE. It can also already identify unnecessary operations at the ends of circuits and remove them.
Results of IQM Deneb
I was able to try five algorithms during my trial. The results of a six-qubit GHZ state were correct and in line with the level of noise you would expect from a superconducting quantum computer before measurement error mitigation is applied. Their QAOA example converged in only about two minutes, which is the fastest I’ve ever seen using real hardware. The SWAP Tests were correct-but-noisy, which is to be expected with the circuit depths associated with SWAP Tests.
Because of the speeds of these experiments, I then began to improvise. A six-qubit Quantum Fourier Transform (QFT) executed, so I then ran a six-qubit Quantum Phase Estimation (QPE) circuit. It executed, too. Because of circuit depths these weren’t meant to be qualitative tests, but rather tests of Deneb’s limits. Again, despite the special purpose for which it was originally intended, it is still a fully capable universal quantum computer.
Conclusion: To Deneb or Not Deneb
With dedicated access – as explained in “Resonating with IQM Resonance” – IQM Deneb is fast. During my trial, I completed 121 jobs, which included 2 runs of their QAOA example. I was watching the job monitor during the QAOA runs, and every few seconds the next iteration queued up. Consequently, as previously noted, 2 Max-Cut problems were solved in about 2 minutes each despite needing 54 and 50 iterations, respectively.
But the real star of the show – and the topology, pardon the pun – is the MOVE operator. Although the transpiler does it better, manual circuit design is enlightening. Once you move a qubit to the central resonator, it suddenly has connectivity with all the other qubits. The most connectivity you’ll find on any other superconducting quantum computer is 1:4, but you may find connectivity as poor as 1:1. In the near future, IQM could potentially offer connectivity of 1:19, which will be really interesting to play with.
Brian N. Siegelwax is an independent Quantum Algorithm Designer and a freelance writer for Inside Quantum Technology. He is known for his contributions to the field of quantum computing, particularly in the design of quantum algorithms. He has evaluated numerous quantum computing frameworks, platforms, and utilities and has shared his insights and findings through his writings. Siegelwax is also an author and has written books such as “Dungeons & Qubits” and “Choose Your Own Quantum Adventure”. He regularly writes on Medium about various topics related to quantum computing. His work includes practical applications of quantum computing, reviews of quantum computing products, and discussions on quantum computing concepts.